Quersummen unter der Lupe
Quersummen werden beim Bearbeiten der Teilbarkeitsregeln in der vierten Klasse thematisiert. Daneben werden sie häufig als Möglichkeit der Selbstkontrolle durch die Schülerinnen und Schüler eingesetzt, können aber auch für Zahlenrätsel oder Zahlenplakate genutzt werden. Vor allem aber lassen sich mit ihnen mathematische Muster und Strukturen entdecken (→ Kaprekar-Konstante). Daher lohnt es sich, Quersummen näher zu betrachten.
Die Quersumme einer Zahl ist die Summe der Werte ihrer Ziffern.
Beispiel: Die Zahl 23 besteht aus den Ziffern 2 und 3. Wenn man diese als Zahlen addiert, also 2 + 3, beträgt die Summe 5. Die Quersumme der Zahl 23 ist dementsprechend 5.
Beim Thematisieren von Quersummen treten typische Stolpersteine auf. Beispiele dafür sind
- einstellige Zahlen („Die Quersumme der Zahl 5 ist 5.“) sowie
- Zahlen mit einer Häufung der Ziffer 0 („Die Quersumme der Zahl 100 ist 1.“).
Wenn man die 0 in die Betrachtungen zu Quersummen aufnimmt, ist sie die einzige Zahl mit der Quersumme 0.
Die Teilbarkeitsregeln für durch 3, 6 und 9 teilbare Zahlen basieren auf Quersummen:
- Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist.
- Eine Zahl ist durch 6 teilbar, wenn ihre Quersumme durch 3 teilbar ist und die Zahl gerade ist.
- Eine Zahl ist durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist.
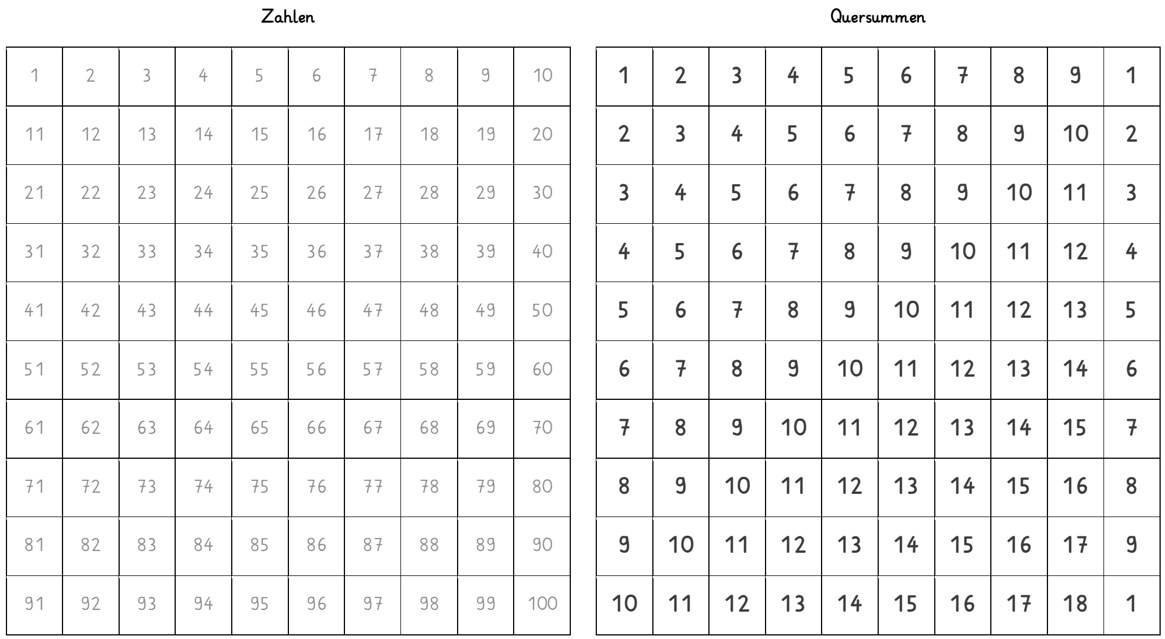
Übersicht über Zahlen bis 100 und ihre Quersummen
siehe auch
Aufgaben der Forscherkartei: Quersummen unter der Lupe
| Aufgabe | Hinweise / didaktischer Kommentar |
|---|---|
| Notiere die Quersummen der Zahlen von 0 bis 20. Zusatz: Bestimme die Quersummen weiterer Zahlen. | Typische Stolpersteine bewusst machen: z.B. einstellige Zahlen, Zahlen mit 0 |
| Notiere die Zahlen der Malfolge der 3 und ihre Quersummen. Beschreibe: Was fällt dir auf? Zusatz: Untersuche weitere Malfolgen und ihre Quersummen. | sich wiederholende Muster entdecken (3, 6, 9, 12, 15, 18, 21 … und QS: 3, 6, 9, 3, 6, 9, 3, …), Bezug zur Teilbarkeitsregel durch 3 |
| Notiere die Zahlen des heutigen Datums (Tag und Monat) hintereinanderweg, ohne Punkte. Beispiel: aus 25.9. wird 259. Bestimme die Quersumme des Datums. Welche Quersumme hat dein Geburtstag? Zusatz: Suche im Kalender das Datum mit der kleinsten und das Datum mit der größten Quersumme. | Differenzierungspotenzial: z.B. nur Tage oder nur Monate untersuchen |
| Notiere eine einstellige Quersumme. Finde passende Zahlen. Zusatz: Wähle eine zweistellige Zahl als Quersumme. Finde passende Zahlen. | vom Probieren zum systematischen Probieren, Reflexion: Wie bin ich vorgegangen? (z.B. „Erst Zehner festlegen, dann Einer ergänzen“: QS 7 → 7, 16, 25, 34, 43, 52, 61, 70) |
| Addiere zu einer Zahl ihre Quersumme. Das Ergebnis ist die neue Startzahl. | Förderung des Kopfrechnens und Bestimmens der Quersumme |
| Subtrahiere von einer Zahl ihre Quersumme. Das Ergebnis ist die neue Startzahl. | Mathematisches Phänomen: „Wir enden immer bei 0.“ → Hintergrund: Nach dem ersten Schritt erhält man ein Vielfaches von 9. Bei Vielfachen von 9 ist auch die Quersumme durch 9 teilbar. So entstehen immer wieder Vielfache von 9, bis das Ergebnis 0 erreicht ist. Differenzierungspotenzial: Vermute: Ist das immer so? (→ unterschiedliche Startzahlen probieren). Gibt es Zahlen, die schneller zur 0 führen als andere? (→ Systematisches Probieren: Wie viele Schritte bis zu 0) |
| Quersummen unter der Lupe. Notiere in einer leeren Hundertertafel für jede Zahl von 1 bis 100 die Quersumme. Untersuche die Quersummen. Was fällt dir auf? Beschreibe. Zusatz: Ordne die Zahlen bis 100 nach ihrer Quersumme. Was stellst du fest? Beschreibe. | Typische Beobachtungen: die Quersummen steigen in jeder Zeile um 1 an → aber Sprung beim Zehner, die Quersummen steigen in jeder Spalte abwärts um 1 an → aber Sprung bei der 100, gleiche Quersummen ergeben eine Diagonale (Ausnahmen bei der 1 in dieser Darstellungsform), es kommen Quersummen von 1 bis 18 vor, Spiegelzahlen (z.B. 23 / 32) haben die gleiche Quersumme, die Quersummen sind nicht gleich verteilt |
| Würfelwettbewerb. Einigt euch, mit wie vielen Würfeln ihr spielen wollt. Hinweis: mindestens drei Würfel. Nun würfelt ihr gleichzeitig mit allen Würfeln. Addiert alle Augenzahlen des Wurfs. Berechnet die Quersumme des Ergebnisses. Wer sie zuerst genannt hat, gewinnt die Runde. Notiert eure Punkte übersichtlich. Wer zuerst 10 Punkte hat, hat gewonnen. Zusatz: Erfindet ein eigenes Rechenspiel mit Quersummen. Notiert die Spielregeln. Probiert es aus. | Förderung des Kopfrechnens und Bestimmens der Quersumme |
| Quersummenzauberei 1. Notiere drei Ziffern. Bilde alle möglichen Zahlen mit diesen Ziffern. Subtrahiere von jeder Zahl ihre Quersumme und notiere die Ergebnisse. Was fällt dir auf? | Ergebnis hat immer die Quersumme 9 → Bezug zur Teilbarkeitsregel durch 9 |
| Quersummenzauberei 2. Notiere eine dreistellige Zahl. Subtrahiere die Quersumme. Teile das Ergebnis durch 9. Bestimme vom diesem Ergebnis wieder die Quersumme und ziehe sie ab. Teile erneut durch 9. Wiederhole so oft, bis du bei 0 ankommst. Zusatz: Probiere es nun mit einer anderen dreistelligen Zahl. | Beispiel 321 321−6=315 315 : 9 = 35 35−8=27 27 : 9=3 3−3=0 Entwicklung von Rechenkompetenz, Bezug zur Teilbarkeitsregel durch 9 Differenzierungspotenzial: die Kinder erkennen selbst, dass dieses wiederholte Vorgehen immer zum Ergebnis 0 führt |
Judith Köhler & Andreas Grajek
Letzte Aktualisierung: 28. Dezember 2025