Entdecken und Experimentieren: Die Kaprekar-Konstante als Übungsformat im Mathematikunterricht
Der indische Mathematiker D. R. Kaprekar entdeckte, dass jede vierstellige Zahl (mit mindestens zwei verschiedenen Ziffern) durch die Anwendung einer bestimmten Schrittfolge zur Zahl 6174 führt. Bei dieser Schrittfolge werden die Ziffern der Zahl absteigend und aufsteigend sortiert, voneinander subtrahiert und der Vorgang mit dem neuen Ergebnis wiederholt. Nach wenigen Wiederholungen bleibt das Ergebnis stabil bei 6174.
Die Kaprekar-Konstante ist die Zahl 6174. Sie ergibt sich durch eine spezielle Schrittfolge beim Rechnen mit vierstelligen Zahlen, die mindestens zwei verschiedene Ziffern enthalten.
Diese Schrittfolge kann im Unterricht als motivierendes Übungsformat für die Subtraktion sowie das Entdecken von Regelmäßigkeiten in Zahlenfolgen eingesetzt werden. Dabei sammeln die Schülerinnen und Schüler spielerisch auch erste Vorerfahrungen mit Konzepten der höheren Mathematik wie Iteration sowie Konvergenz, deren späteres Verständnis hier angebahnt werden kann (vgl. → Ungelöste Probleme der Mathematik).
Hintergrund zur Kaprekar-Konstante
Die Kaprekar-Konstante 6174 wird durch die Anwendung eines iterativen (wiederholten) Verfahrens erreicht, bei dem die Ziffern einer vierstelligen Zahl auf- und absteigend sortiert und anschließend voneinander subtrahiert werden. Unabhängig von der Ausgangszahl (solange sie nicht aus identischen Ziffern besteht) führt dieser Prozess nach maximal sieben Iterationen immer zur Zahl 6174.
Beispiel: Startzahl 3524
Schritt 1: Ausgangszahl 3524
- absteigend sortiert: 5432
- aufsteigend sortiert: 2345
- Differenz: 3087
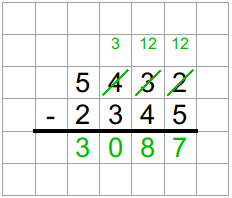
Schritt 2: neue Zahl 3087
- absteigend sortiert: 8730
- aufsteigend sortiert: 0378
- Differenz: 8352
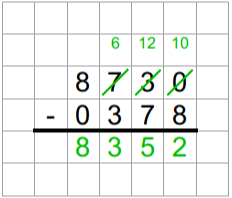
Schritt 3: neue Zahl 8352
- absteigend sortiert: 8532
- aufsteigend sortiert: 2358
- Differenz: 6174
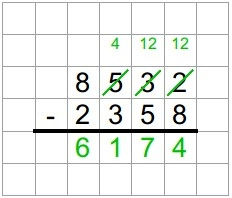
Nach drei Schritten bleibt das Ergebnis des Beispiels mit der Startzahl 3524 bei weiteren Wiederholungen stabil, da die nächsten Differenzen immer wieder zu 6174 führen (7641 – 1467 = 6174). Diese Stabilität wird als Konvergenz bezeichnet.
In der Grundschule werden diese Konzepte nicht explizit behandelt oder thematisiert. Durch das spielerische Arbeiten mit der Kaprekar-Konstante erkennen die Kinder allerdings, dass das ständige Wiederholen der gleichen Schritte zu einer festen Ergebniszahl führt, was (später in der weiterführenden Schule und darüber hinaus) das Verständnis für Konvergenz (Annäherung an einen stabilen Wert) fördern kann. Damit wird auch schon im Mathematikunterricht der Grundschule die Entwicklung eines Grundverständnisses für algorithmische Ansätze sowie das Computational Thinking im Sinne informatischer Grundbildung gefördert.
Übungsformat: Wettlauf zur 6174
Der „Wettlauf zur 6174“ ist ein Übungsformat, bei dem Schülerinnen und Schüler eigenständig Zahlen auswählen und die zur Kaprekar-Konstante führende Schrittfolge ausführen (ordnen und subtrahieren). Die Aufgabe besteht darin, die verschiedenen Schritte zu notieren und ggfls. nach bestimmten Mustern zu suchen.
Dabei kann ein motivierender Wettbewerb entstehen, um beispielweise herauszufinden
- bei welchen Zahlen die Kaprekar-Konstante 6174 mit der maximalen Anzahl an Iterationsschritten erreicht wird (→ sieben Schritte),
- welche Zahlen die Kaprekar-Konstante in nur wenigen Schritten erreichen (z.B. zwei oder drei Schritte),
- welche Zahlen die kürzeste Iterationsfolge (ein Schritt) aufweisen.
Einstieg
Die Lehrkraft beginnt die Unterrichtseinheit:
Ich möchte euch von einem Mathematiker erzählen: Dattathreya Ramachandra Kaprekar. Er liebte es, mit Zahlen zu spielen und zu experimentieren. Dabei machte er eine spannende Entdeckung:
Wenn man die Ziffern einer Zahl in einer bestimmten Weise sortiert und dann subtrahiert, passiert etwas Magisches. Egal mit welcher Zahl man startet, landet man am Ende immer bei derselben Zahl! Sie lautet 6174.
Ihr werdet nun selbst herausfinden, wie das funktioniert:
- Denkt euch eine beliebige vierstellige Zahl aus. Achtet darauf, dass nicht alle Ziffern gleich sind – es müssen mindestens zwei verschiedene Ziffern vorkommen.
- Ordnet nun die Ziffern eurer Zahl einmal der Größe nach von der größten zur kleinsten Ziffer. Schreibt diese Zahl auf.
- Ordnet die Ziffern nun von der kleinsten zur größten Ziffer. Schreibt auch diese Zahl auf.
- Als nächstes bildet ihr die Differenz der beiden Zahlen: Subtrahiert die kleinere von der größeren Zahl.
- Wiederholt diesen Vorgang mit dem Ergebnis: Ordnet die Ziffern der Größe nach, dann in umgekehrter Reihenfolge, und subtrahiert erneut.
- Setzt diese Schritte fort, bis sich das Ergebnis nicht mehr ändert. Was stellt ihr fest?
Ich bin gespannt, was ihr herausfindet! Probiert es mit verschiedenen Startzahlen aus.
Arbeitsphase
Jedes Kind oder jede Gruppe wählt eine Startzahl und beginnt mit der Schrittfolge. Dabei notieren die Kinder die Rechenschritte bis zur 6174.
Differenzierungsmöglichkeiten
- Beginn mit einer gemeinsamen Startzahl, z.B. 3524
- die Kinder finden die „magische Zahl“ selbst heraus
- Zuordnung von Zahlen mit einer bestimmten Schrittanzahl an Kinder bzw. Gruppen (siehe Ergebnissicherung)
- Startzahlen, die mit vielen oder wenigen Schritten zur 6174 führen
- Herausfinden der maximal möglichen Anzahl an Schritten
- Startzahlen, die in genau einem Schritt zur 6174 führen
- Startzahlen, die in genau sieben Schritten zur 6174 führen
- Startzahlen, die mit zwei (drei, vier, fünf, sechs) Schritten zu 6174 führen
- kleinste vierstellige Startzahl mit dem längsten Weg
- größte vierstellige Startzahl mit dem kürzesten Weg (→ siehe Hinweise: nur bei systematischem Probieren der gesamten Lerngruppe von der Startzahl 9998 aus abwärts herauszufinden)
- Untersuchung besonderer Jahreszahlen als Startzahlen (wie z.B. eigenes Geburtsjahr, das aktuelle Jahr 2024 → 4 Schritte, das bevorstehende Jahr 2025 → 6 Schritte)
Ergebnissicherung
An der Tafel oder auf einem Plakat der Gruppe werden die Ergebnisse zusammengetragen und übersichtlich dargestellt:
Startzahlen und deren Schritte bis zur 6174
| 1 Schritt | 2 Schritte | 3 Schritte | 4 Schritte | 5 Schritte | 6 Schritte | 7 Schritte |
| 4369 6406 4282 | 9173 5874 4587 | 6993 1434 1783 | 9605 9757 4047 | 2469 8272 7804 | 2129 6918 3706 | 9160 9039 7341 |
Austausch und Reflexion
Gemeinsam wird diskutiert, ob alle untersuchten Zahlen am Ende zur 6174 führen und wie viele Schritte dafür nötig waren. Die Ergebnisse können in einer Tabelle festgehalten werden, um zu visualisieren, wie viele Zahlen nach einem, zwei, drei oder mehr Schritten die 6174 erreichen.
Anhand dieser Übersicht lassen sich Besonderheiten leichter erkennen: Lässt sich sagen, ob es Startzahlen gibt, die besonders schnell (oder langsam) zur 6147 führen? Was haben die Ergebniszahlen / die Zahlen einer Spalte / … gemeinsam? Dabei wird das mathematische Verständnis, der Zahlenblick und der Austausch über Mathematik gefördert.
siehe auch
Spannende Beispiele
Die kleinste Startzahl mit dem längsten Weg (7 Schritte): 1004
- 1. Schritt: 4100 – 0014 = 4086
- 2. Schritt: 8640 – 0468 = 8172
- 3. Schritt: 8721 – 1278 = 7443
- 4. Schritt: 7443 – 3447 = 3996
- 5. Schritt: 9963 – 3699 = 6264
- 6. Schritt: 6642 – 2466 = 4176
- 7. Schritt: 7641 – 1467 = 6174
Die größte Startzahl mit dem kürzesten Weg (1 Schritt): 8532
- 1. Schritt: 8532 – 2358 = 6174
Hinweise
- Die Subtraktion von Zahlen mit vier gleichen Ziffern (1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999) führt nicht zur Kaprekar-Konstante, sondern zur Null (1111 – 1111 = 0).
- Es gibt insgesamt 8991 vierstellige Zahlen, die durch das wiederholte Anwenden der Kaprekar-Schrittfolge zur Zahl 6174 führen.
- Je nachdem, ob zuerst die absteigende oder aufsteigende Zahl gebildet wird, kann die jeweils andere Zahl auch als deren Spiegelzahl bezeichnet werden.
- Im Unterricht muss nicht von „Kaprekar-Konstante“ gesprochen werden. Auch der Begriff „Kaprekar-Zahl“ sollte vermieden werden, da er in der Mathematik eine andere Bedeutung hat. Stattdessen bietet es sich an, von der „besonderen Zahl 6174“, der „magischen Zahl 6174“ o.ä. zu sprechen.
- Eine spannende Feststellung ist, dass alle nach der Schrittfolge erzeugten Differenzen durch 9 teilbar sind (einschließlich der Kaprekar-Konstante selbst). Das liegt daran, dass die Differenz zweier Zahlen mit identischer Quersumme durch 9 teilbar ist. Somit dient die Beschäftigung mit der Kaprekar-Konstante auch der Anwendung und dem Verständnis von Teilbarkeitsregeln.
- Permutationen: Jede mögliche Umstellung der Ziffern von 6174 (wie z. B. 7641, 4716 oder 1467) führt als Startzahl bereits in einem einzigen Schritt zur Kaprekar-Konstante. Hintergrund ist, dass diese Permutationen dieselben Ziffern wie 6174 enthalten und daher die gleiche Differenz erzeugen, wenn sie absteigend und aufsteigend sortiert und subtrahiert werden. Auch alle Permutationen z.B. der Zahl 8532 führen bereits nach einem Schritt zur Differenz 6174. Dies lädt dazu ein, systematisch mit Zahlen aus denselben Ziffern zu experimentieren, um diesen Zusammenhang zu entdecken, der auch für Startzahlen gilt, die zu längeren Schritten bis zur Kaprekar-Konstante führen.
- Beim Vergleich der Rechenwege für Zahlen mit unterschiedlichen Schrittzahlen lässt sich eine interessante Beobachtung machen: Die Rechenwege für Zahlen mit vielen Schritten enthalten oft Teilsequenzen, die identisch mit den kompletten Rechenwegen von Zahlen mit weniger Schritten sind. Diese Beobachtung kann genutzt werden, um für das Erkennen von Mustern und Strukturen zu sensibilisieren.
Mehr als Rechnen: Mathematisches Denken entwickeln
Die Beschäftigung mit der Kaprekar-Konstante im Mathematikunterricht der Grundschule ist eine motivierende Möglichkeit, um das Verständnis für die Subtraktion zu festigen und die Freude am Entdecken mathematischer Phänomene zu wecken. Indem die Kinder mit Ziffern und Zahlen experimentieren und ihre Ergebnisse reflektieren, lernen sie zudem spielerisch die erst viel später relevant werdenden Grundzüge von Konvergenz und Iteration sowie grundlegende Denkstrukturen kennen, die ihnen bei der Orientierung und Mitgestaltung in einer zunehmend digitalisierten Welt helfen. Auf diese Weise wird Mathematik als kreativer Umgang mit Zahlen, aber vor allem als „Muster und Strukturen“ erlebbar – ganz im Sinne von Kaprekar, der die Freude am Forschen und Staunen fördern wollte.
Andreas Grajek
Letzte Aktualisierung: 6. Januar 2025