Unterricht als Ausgangspunkt für eigene Entdeckungen: Diagonalen in n-Ecken
Angeregt von einer mathematischen Unterrichtseinheit zu ebenen Figuren in Klassenstufe 3 vertiefte sich ein Schüler in eigene Überlegungen bezüglich n-Ecken bzw. „Vielecken“. Systematisch und übersichtlich notierte er sein Vorgehen, um einem möglichen Zusammenhang von Ecken, Seiten und Diagonalen (als Verbindungen nicht benachbarter Punkte) in „Vielecken“ nachzuspüren.
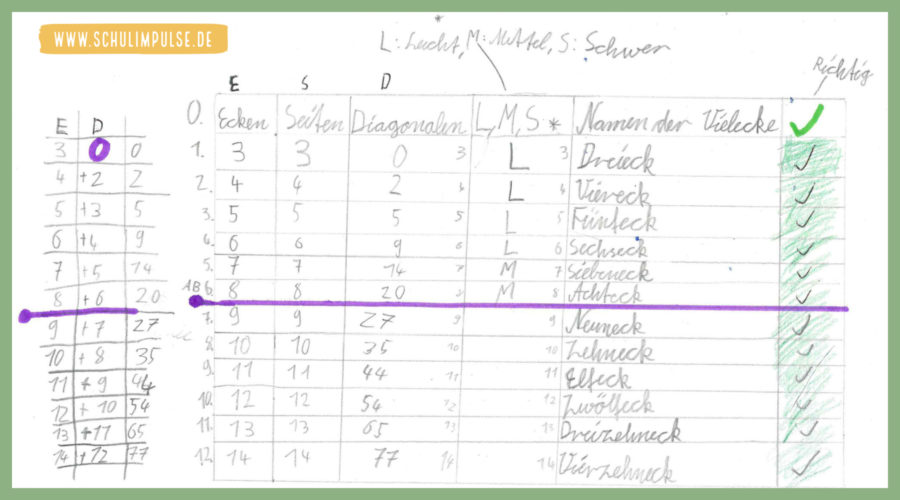
Zunächst beobachtete H., dass die Diagonalenanzahl, beginnend beim Dreieck mit 0 Diagonalen, sich mit jedem hinzukommenden Eckpunkt um einen bestimmten Wert erhöht. Bis zum 9-Eck überprüfte er diese Vermutung auch zeichnerisch, bevor er sie in seine Tabelle eintrug.
| Ecken | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Diagonalen | 0 | 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | 54 | 65 | 77 |
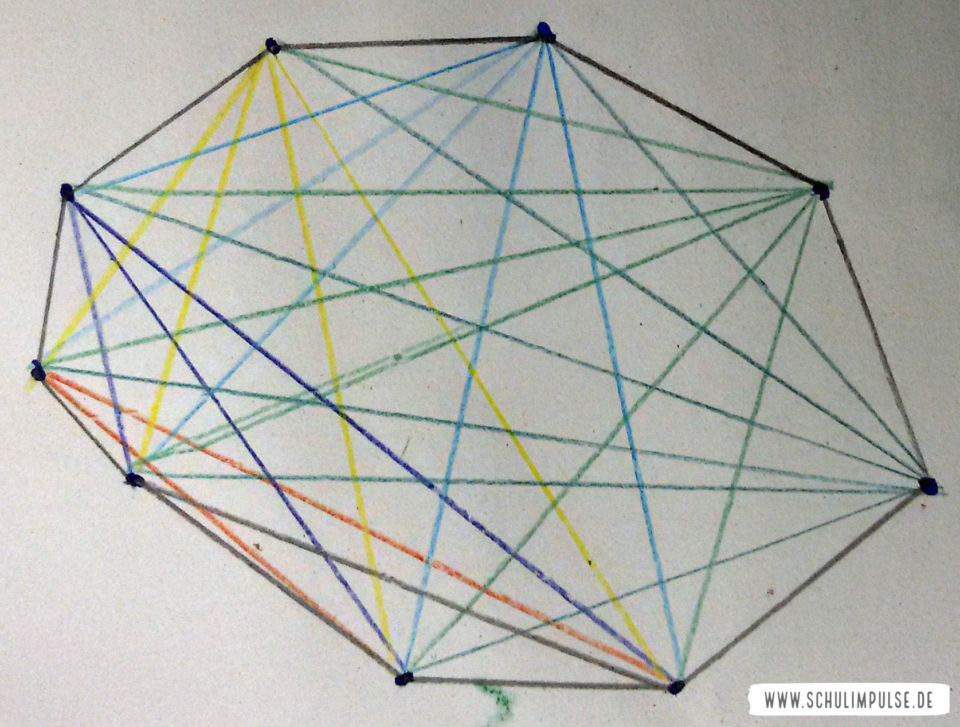
Mittels einer weiteren Übersicht verdichtete und verdeutlichte er seinen Verdacht, dass tatsächlich eine Beziehung zwischen der Ecken-, Seiten- und Diagonalenanzahl in Vielecken besteht. Mit jedem zusätzlichen Eckpunkt erhöht sich auch die entsprechende Anzahl an hinzukommenden Diagonalen um jeweils 1. Somit war nun klar, wie viele Diagonalen beispielsweise ein 15- oder 16-Eck hat; die Tabelle lässt sich beliebig fortsetzen.
| Ecken | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| hinzukommende Diagonalen | 0 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 | +10 | +11 | +12 |
| Diagonalen | 0 | 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | 54 | 65 | 77 |
Offen blieb noch die Frage, wie sich die Anzahl der Diagonalen in Vielecken berechnen lässst. Denn ohne weiteres lässt sich z.B. die Anzahl der Diagonalen eines 154-Ecks mit der Tabelle nicht erkennen – es sei denn, man setzt sie immer weiter fort. Hier kommt der Lehrer wieder ins Spiel, dem verschiedene Möglichkeiten offenstehen, den Schüler zu weiteren Erkenntnissen anzuregen oder den bisherigen Lernprozess in einen Gesamtkontext einzuordnen und die angewandten Arbeitstechniken und Herangehensweisen des Schülers gemeinsam zu reflektieren und zu bewerten.
Folgende Überlegungen helfen bei der Berechnung der Diagonalen im n-Eck und können bei sich bietender Gelegenheit mit dem Schüler in angemessener Weise thematisiert werden:
- Man hat n Punkte.
- Jeder Punkt kann mit jedem anderen Punkt verbunden werden, außer mit sich selbst: also n mal (n-1).
- Der „Vorgänger- und Nachfolger-Punkt“ darf auch nicht mit verbunden werden, da das die Seiten des n-Eckes sind: also n mal (n-3).
- Man darf jede Diagonale nur einmal zählen (denn sie kann ja von Punkt a zu b gehen und auch umgekehrt) – also das Ganze geteilt durch 2, also n mal (n-3) und das durch 2.
- Die fertige Formel:
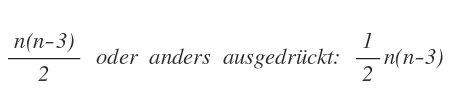
siehe auch
Letzte Aktualisierung: 23. Januar 2023